原标题：如何传小纸条才能不被老师发现？

从技术角度讲，学生可以通过加密手段避免老师知道纸条内容。

假设学生叫做Alice和Bob，而老师叫Evil，Alice要把纸条传给Bob，但是Evil可能偷看纸条内容并拍照发到微信群。

怎么才能防止Evil偷看呢？Alice可以对信息进行加密。

有一天放学的时候，Alice偷偷告诉Bob：以后我给你写的话都会往后推一个字母，比如L就变成了M，o就变成了p，v就变成了w，e就变成了f。你收到纸条之后，就把纸条内容减去一个字母，就知道我想说什么了。这样一来，就算Evil偷看了我们纸条上的内容，也不知道我们要说什么。

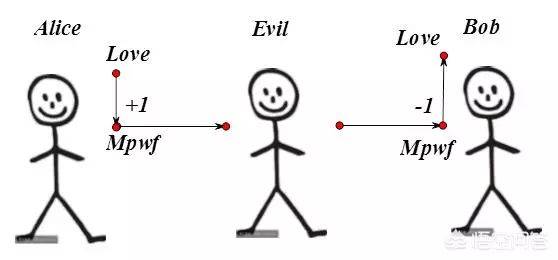
以上的过程，就是密码学中最基本的加密算法：对称加密。也就是说，我们把明文（Love）按照一定的密钥（1）加密成密文（Mpwf），对方接收后再利用同样的密钥（1）进行解密，就再次得到明文（Love）。

但是这种加密方法面临很多的问题。比如，Evil虽然不知道密钥是什么，但是他可以一次次的用各种方法尝试密钥。比如：在英文中26个字母出现的频率是不同的。只要截获了大量的密文，就可以利用频率法猜出密钥，从而破解密码。

为此，Alice和Bob只好不停地更换密钥，每天晚上放学都要商量一下第二天的密钥是什么。但是万一哪天两人放学没有商量好，或者商量密钥的时候被Evil偷听到了，那他们的密码就又有可能被破译。商量密钥的过程就称为密钥分发，而密钥分发是对称加密算法最大的风险。

那怎么办呢？

有一天两人想出了一种新的方法：首先Bob拿着一个没有锁上的空盒子，这个盒子只要一扣就可以锁上。他让Evil把箱子传给Alice，然后Alice把小纸条放进盒子里，把盒子扣上。再通过Evil把盒子传给Bob。盒子的钥匙只有Bob有，Bob拿到盒子之后用钥匙打开，就可以拿到小纸条了。

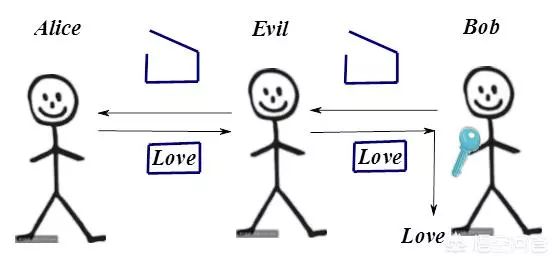
这种方式就是现代更加保密的加密方式：非对称加密。也就是加密过程（锁箱子）方法是公开的，而解密过程使用的密钥（钥匙）是不公开的，而且加密过程的密钥（锁）和解密过程的密钥（钥匙）并不相同。Evil可以截获箱子，也知道加密方法，但是由于没有钥匙，他无法打开箱子，所以就不知道信息内容是什么意思了。

有同学可能要问，那么Evil不能通过一次次尝试试出钥匙吗？这就取决于这把锁是否足够复杂了。

在当今的数学发展中，人们已经知道了大数的质因数分解非常困难， 在密码学中就是利用了这一点设计的加密和解密算法。这种算法除了穷举还没有找到更快的计算方式，而穷举所需要花的时间非常长，从而保证了密码安全。而且，Bob可以不停的更换锁头和钥匙，这个过程无需与Alice进行沟通，也就解决了密钥分发的问题。

那么，具体的过程是怎么实现的呢？我们来介绍一种经典的加密算法：RSA算法。

RSA算法是1977年麻省理工学院的三名数学家罗纳德、萨莫尔阿德曼一起提出的，RSA就是他们三个名字的第一个字母。这种加密算法基于欧拉定理等数学工具。具体算法是：

假如Alice要把一个数字m传输给Bob，那么过程是这样的：

Bob要做的事（制作密钥）：

1. 首先写出两个质数p、q
2. 计算二者成绩n=pq
3. 计算欧拉函数f(n)=(p-1)(q-1)（欧拉函数是有具体含义的，但是不了解这个含义并不影响我们理解算法）
4. 在1到f(n)之间取一个数字e，使得e与f(n)互质。（所谓互质，就是除了1以外e和没有其他公约数）
5. 找到另一个整数d，使得ed-1是的整数倍
6. （这时e和d称为模反素数，这个求解过程并不复杂）
7. Bob将数字e、n通过公开方式传递给Alice

Alice要做的事（加密）：

1. Alice拿到e和n之后，计算m的e次幂除以n所得到的余数c
2. Alice将c作为密码通过公开场合发送给Bob

Bob拿到c之后要做的事（解密）：

计算c的d次幂除以n的余数，数学上可以证明：这个余数就是m。

在这个过程中，Evil可以截获大数n、公钥e和密文c，如果要解密，必须使用私钥d。如果要计算私钥d，必须知道f(n)，由于f(n)=(p-1)(q-1)，要知道f(n)，必须知道p和q。又因为n=pq，要知道p和q，就必须对n进行质因数分解。

大数的质因数分解非常困难，计算一个费马数都花了90年的时间。现在有了计算机，计算能力飞速提高，但是报道过的曾被破解的RSA算法中n最大只有768位二进制数，而现在所使用的RSA算法大数n普遍有1024、2048或4096位二进制数，这么大的数字在有限的时间内计算机也无法进行质因数分解，于是就保证了密码的安全性。

不过，根据科学家的研究，如果量子计算机被发明出来，大数的质因数分解时间就会大大缩短，那么传统密码就可能面临风险。不过大家不用担心，到时候科学家们会想出更好的方法进行加密的。